Mathematica and Python Nanodegree cont’d…

Nanodegree

• We’re doing fun stuff like this in Python!

A movie site that shows images of movies you like, and gives descriptions

Click on the image and it will play the trailer!

• Learning about classes and objects, and how to instantiate so that they call on different objects.

Teaching myself Mathematica

• In the midst of my Nanodegree and before my C++ class continues, I thought that I should use a 15-day trial of Mathematica.

Wait..what is Mathematica?

• It’s a tool used for numerical computation, data visualization, primarily used by mathematicians, scientists and engineers. It is known for its precision and was invented by Stephen Wolfram.

• Here is the wiki

But why?

• Here is a great article on who uses Mathematica.

• There is also quite an active Mathematica Stack Exchange. Do subscribe!

• It’s always been something I’ve been interested in learning a bit of; I can’t put my finger on why right now.

• That being said, I did finish a project early, and I only have a 15-day trial, so I thought that this would be perfect timing.

So…

• My beginnings were from this tutorial

• I liked it so much, I bought a book on it, and plan on continuing, taking baby steps to learn.

It’s like Matlab, LaTeX and Jupyter had a baby!

• Seriously, if you’re familiar with those, things will seem very familiar! It’s super fun!

• I’m still learning, but here’s some of what I learned today!

Defining and getting used to Syntax

Algebra using power and subscripting (very similar to LaTeX)

\

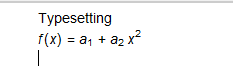More typesetting

• Whoops, I forgot a bracket!

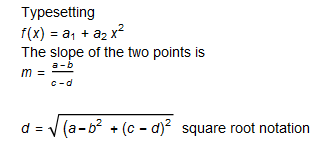
Precision in calculations (this is with 30 digits of precision)

One-based indexing

Appending to a list

Appended List with pi and finding the Length of a List

Substitution

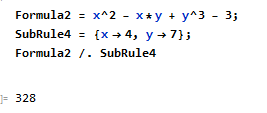
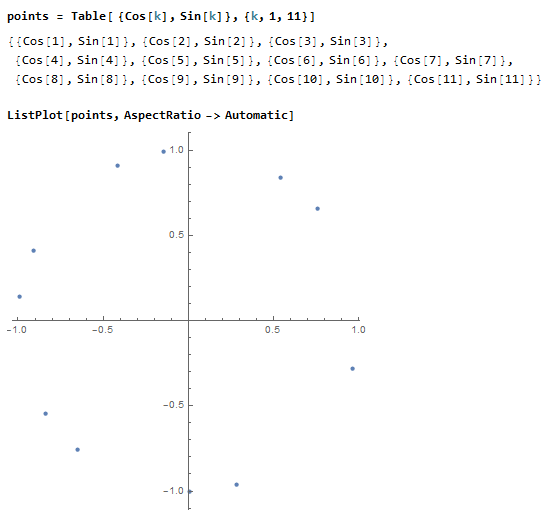
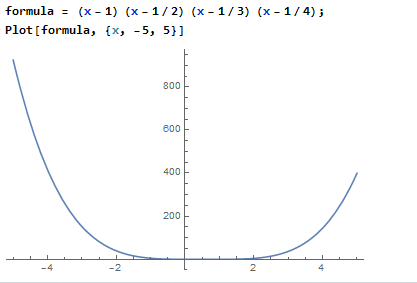
Plotting a function

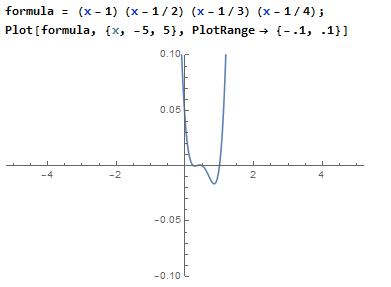
Defining the Plot Range

Adding Details to the Plot

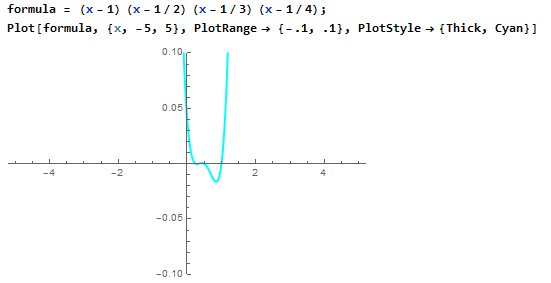
Functions Learned

Alt+7 -> Enter mode 
Ctrl + ( -> Math mode 
Ctrl + _ -> subscript
Ctrl + space -> out of subscript mode 
Ctrl + ^ -> power 
Ctrl + / -> (fractions) and arrow down for denominator
Ctrl + 2 -> square root
Alt + 7 -> type words (not mathematical commands)
Shift + Enter -> Evaluate
Alt + . -> Abort Computation

a2 = N[2, 20] -> 2 means 2 is numerical
and 20 is accuracy (ie 20 decimals)

------------------------------

one-based indexing
Length[Listname] -> gives length of list

---------
Plotting 
---------
functiontoplot = x + 5 
Plot[function, {x, value, value}, PlotRange->
{range1, range2}, PlotStyle->{Thick,Color}]

Two figures overlapping -> Show[Figure1, Figure2]

Things to do

• Continue with Nanodegree (finish up lessons and get to Project by end of this week..hopefully)
• Finish Application (probably will be done by Wednesday)
• Continue with Mathematica tutorials and experimentation (when you obtain book, read and work through)

Katas

• Create a pattern that looks like

1
22
333
4444
55555

• My solution

def pattern(n):
    arr = ""
    if n < 1:
      return ""
    elif n == 1:
      return "1"
    else:
      for i in range(2, n+1):
        arr =  arr + "\n" + str(i) * (i)
    return "1" + arr

• Find first non-consecutive number

def first_non_consecutive(arr):
    arr1 = []
    arr2 = []
    a = arr[0]
    b = arr[-1]
    
    # find full list with no elements left out
    for i in range(a, b+1):
      arr1.append(i)
      
    # find list difference between two lists
    d = list(set(arr1) - set(arr))
    e = sorted(d)
    # value is one more than the difference
    try:
      return e[0]+1
      # catch values where the lists are the same
    except:
      return None